Floor Tiles

题目大意

给定一棵所有边权为$1$的树，定义$f(u) = \sum_{v} dis(u,v)$，$v$表示树中所有节点，$dis(u, v)$是指节点$u$到节点$v$之间的简单路径的长度。

给出一个整数$x(1 \le x \le 10^{18})$，如果一棵树中存在两个节点使得$f(u) - f(v) = x$，则称这棵树为“好树”，求构造出一棵“好树”所需的最小节点数。

解题思路

首先考虑$n$个节点所能构造出的$f$的最大差值，很明显，形成一条链的时候差值最大，可以选取端点和最中间的点，可以得到最大差值$w = \lfloor\frac{n - 1}{2}\rfloor \cdot \lceil\frac{n - 1}{2}\rceil$，接下来思考对这条链上加点，具体对以下这条链进行操作：

t1

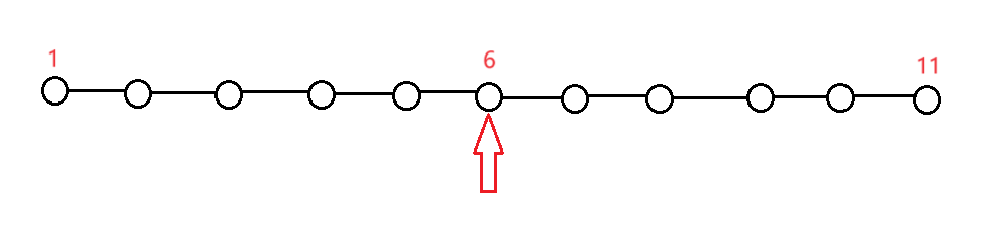
首先选取节点$1$和节点$6$，此时$w = 5 \times 5 = 25$，然后我们可以在$6$的右边多连一个点，或者在$1$的左边多连一个点，或者在节点$1$到节点$6$的之间的简单路径上加点。然而在$6$的右边和在$1$的左边加点是等效的，因为，当在节点$1$到节点$6$的简单路径上没有多余的分叉的话，这两个点对应的$f$差值$w = d(\vert u_1 - u_6\vert)$，其中$d$是指这两个点之间的简单路径长度，$u_i$是指除去在简单路径上与$i$相连的点的个数。所以这两者是等效的。

接下来对路径上加点和非路径上加点进行讨论，首先是在路径上加点：

t2

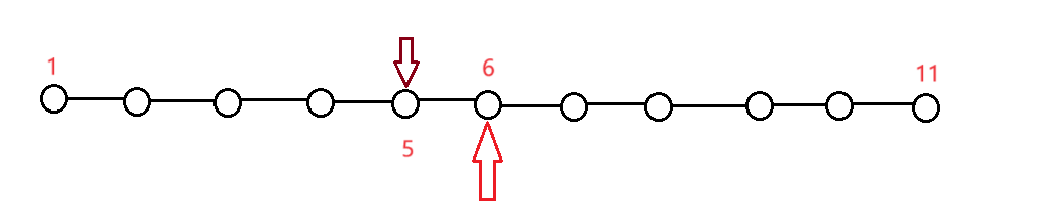
如果我们在节点$5$上向外连点，则$w$变为$25 + 3 = 28$，同理如果在节点$4$上向外连点，则$w$变为$25 + 1 = 26$；

然后是在非路径上加点，整个图的$w’ = 5 \times 6 = 30$。

这个时候发现，在区间$[26, 30]$上，并且整棵树的大小为$n + 1$时，$w$取不到$27$和$29$，又由于大小为$n$时$w$最大为$25$，所以只能考虑$n+2$及以上的情况，可以将选取的节点$6$往后挪一位挪到节点$7$，这个时候$w = 24$，经过手玩发现，在路径上加$2$个点可以将剩下的情况(即$27$和$29$)取到。

然后继续在节点为奇数个，且中间点到端点的简单路径长度为偶数时，与上面的分析类似。

最后再讨论节点为偶数个的情况，发现，加一个点可以将区间$[w + 1, w’]$上的值全部取到。

根据数学归纳法以及整合以上信息，最终可以得到一个这样的做法：先求出满足$f$最大差值小于等于$x$的最大$n$，再对$n$分奇偶讨论，对$n$为奇数的时候再对中间点与端点距离的奇偶进行讨论，这里可以整合为，$x$为偶数时，答案为$n + 1$，否则为$n + 2$。不太懂的可以看一下这份提交记录，对照一下就懂了。

提交记录

注意求$n$时不能直接用$sqrt$，因为$double$只有在有效数字在$15 - 16$以下才能保证精度。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
#define maxn 200100
#define int long long
using namespace std;
const double eps = 1e-8;
int a[maxn];

int sqr(int x){
	int l = 1, r = 1e9 + 10;
    while(l <= r) {
        int mid = l + r >> 1;
        if(mid * mid <= x)  l = mid + 1;
        else  r = mid - 1;
    }
	return r;
}

void solve(){
    int x;  cin >> x;
    int t1 = sqr(x), t2 = t1;
    if(t1 * (t1 + 1) <= x)  t2++;
    int n = t1 + t2 + 1;
    if(t1 * t2 == x)  cout << n << '\n';
    else if(t1 != t2)  cout << n + 1 << '\n';
    else if(t1 == t2) {
        if(x % 2 == 0)  cout << n + 1 << '\n';
        else  cout << n + 2 << '\n';
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);  cout.tie(0);
    int t = 1;  cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}