题目大意 平面直角坐标系上有$n(1 \le n \le 2 \times 10^3)$个矩形,对于$k\in[1,n]$,求解在$n$个矩形中随机选取$k$个不同的矩形,其所有覆盖部分的并集的面积的期望值,由于答案可能很大,请对$998244353$取模。
解题思路 官方题解的做法是用任选的方案数减去没有被覆盖的方案数,思路比较清晰简单。奈何笔者赛时并没有想到,一直在用容斥的思想去写,所幸最后还是写了出来。笔者认为还算是一次较为有益的尝试,所以这篇博客主要探究容斥的做法,至于此题的具体做法将不再赘述。
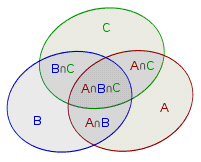
考虑从$n$个矩形里面取出$i$个矩形,然后参考这样一个经典的图,
可以将$A$、$B$和$C$分别看作一个矩形所覆盖的区域,它们之间有部分相互重叠,并假设当前$n$为$3$,要从这三个矩形里面取$i$个矩形,并求它们覆盖面积的期望。
首先参考这张图里的容斥公式:
$\vert A\cup B\cup C \vert = \vert A\vert + \vert B\vert +\vert C\vert - \vert A\cap B| - \vert A\cap C\vert - \vert B\cap C\vert + \vert A\cap B\cap C\vert$
假设被这三个矩形覆盖$1$、$2$和$3$次的面积分别为$S_1$、$S_2$和$S_3$,那么上面的容斥就可以用另一种形式来表现:
$C_{1}^{1}S_1C_{3 - 1}^{i - 1} + C_{2}^{1}S_2C_{3 - 1}^{i - 1} + C_{3}^{1}S_3C_{3 - 1}^{i - 1} - C_{2}^{2}S_2C_{3 - 2}^{i - 2} - C_{3}^{2}S_3C_{3 - 2}^{i - 2} + C_{3}^{3}S_3C_{3 - 3}^{i - 3}$
对于$C_{1}^{1}S_1C_{3 - 1}^{i - 1} + C_{2}^{1}S_2C_{3 - 1}^{i - 1} + C_{3}^{1}S_3C_{3 - 1}^{i - 1}$这一块可以看作是计算任选一块矩形,其所覆盖的区域对答案的贡献,$C_{1}^{1}S_1$表示从仅被一个矩形覆盖的区域上选择覆盖了这一块区域的其中一块矩形的方案数,$C_{2}^{1}S_2$表示从仅被两个矩形覆盖的区域上选择覆盖了这一块区域的其中一块矩形的方案数,$C_{3}^{1}S_3$也是类似的道理。至于$C_{3 - 1}^{i - 1}$,因为总共要选$i$个矩形,现在已经确定了一个,那么还要从剩下的矩形里再选$i - 1$个。
然后,就会发现这一块$C_{1}^{1}S_1C_{3 - 1}^{i - 1} + C_{2}^{1}S_2C_{3 - 1}^{i - 1} + C_{3}^{1}S_3C_{3 - 1}^{i - 1}$与容斥中$\vert A\vert + \vert B\vert +\vert C\vert$这一块的意义是等价的
这一块$(- C_{2}^{2}S_2C_{3 - 2}^{i - 2} - C_{3}^{2}S_3C_{3 - 2}^{i - 2})$则等价于$(- \vert A\cap B| - \vert A\cap C\vert - \vert B\cap C\vert)$
剩下的$C_{3}^{3}S_3C_{3 - 3}^{i - 3}$则等价于$\vert A\cap B\cap C\vert$
那么我们就可以通过容斥的这种思想推广出这样的式子:
$从n个矩形中任取i个矩形,它们交的总和 = \sum_{j = 1}^{i}(-1)^{j}C_{n - j}^{i - j}\sum_{k = j}^{n}C_{k}^{j}S_k$
最终求期望的公式便为:
$res_i = \frac{\sum_{j = 1}^{i}(-1)^{j}C_{n - j}^{i - j}\sum_{k = j}^{n}C_{k}^{j}S_k}{C_{n}^{i}}$
由于还需要从$1$到$n$遍历$i$的取值再加上快速幂求逆元,看起来时间复杂度是$O(n^3logn)$,但实际上通过观察发现,$\sum_{k = j}^{n}C_{k}^{j}S_k$这一块的值是固定的,所以可以先预处理,最终时间复杂度为$O(n^2logn)$。
笔者的数学功底较为薄弱,对于想法的表述实在是只能做到这样。如果你对这种做法有什么独到的见解或看法的话,欢迎给出意见或指导,笔者会尝试着继续努力的。
参考代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 #include <bits/stdc++.h> #define maxn 4010 #define int long long using namespace std;const double eps = 1e-8 ;const int mod = 998244353 ;int s[maxn][maxn], C[maxn][maxn];int x1_[maxn], y1_[maxn], x2_[maxn], y2_[maxn];int nx[maxn], ny[maxn];int tt[maxn], res[maxn];int qmi (int a, int b, int m) int res = 1 ; a %= m; while (b) { if (b & 1 ) res = res * a % m; a = a * a % m; b >>= 1 ; } return res; } void solve () map<int , int >xs, ys; set<int > numx, numy; int n; cin >> n; for (int i = 1 ; i <= n; ++i) { cin >> x1_[i] >> y1_[i] >> x2_[i] >> y2_[i]; numx.insert (x1_[i]); numy.insert (y1_[i]); numx.insert (x2_[i]); numy.insert (y2_[i]); } int curx = 0 , cury = 0 ; for (auto u : numx) { xs[u] = ++curx; nx[curx] = u; } for (auto u : numy) { ys[u] = ++cury; ny[cury] = u; } for (int i = 1 ; i <= n; ++i) { s[xs[x1_[i]]][ys[y1_[i]]]++; s[xs[x2_[i]]][ys[y1_[i]]]--; s[xs[x1_[i]]][ys[y2_[i]]]--; s[xs[x2_[i]]][ys[y2_[i]]]++; } for (int i = 1 ; i < curx; i++) { for (int j = 1 ; j < cury; j++) { int dx = nx[i + 1 ] - nx[i]; int dy = ny[j + 1 ] - ny[j]; s[i][j] = s[i][j] + s[i - 1 ][j] + s[i][j - 1 ] - s[i - 1 ][j - 1 ]; tt[s[i][j]] = (tt[s[i][j]] + dx * dy % mod) % mod; } } for (int i = 1 ; i <= n; ++i) { for (int j = i; j <= n; ++j) { res[i] = (res[i] + C[j][i] * tt[j] % mod) % mod; } } for (int i = 1 ; i <= n; ++i) { int ans = 0 ; for (int j = 1 ; j <= i; ++j) { int tmp = C[n - j][i - j]; if (j & 1 ) ans = (ans + tmp * res[j] % mod) % mod; else ans = ((ans - tmp * res[j] % mod) % mod + mod) % mod; } ans = ans * qmi (C[n][i], mod - 2 , mod) % mod; cout << ans << '\n' ; } } signed main () ios::sync_with_stdio (false ); cin.tie (0 ); cout.tie (0 ); for (int i = 0 ; i <= 2000 ; ++i) { for (int j = 0 ; j <= i; ++j) { if (j == 0 || j == i) C[i][j] = 1 ; else C[i][j] = (C[i - 1 ][j - 1 ] + C[i - 1 ][j]) % mod; } } int t = 1 ; while (t--) { solve (); } return 0 ; }